C'est loin la mer?

Question :

Quelle est la commune française la plus éloignée de la mer ?

Pour le savoir , il va falloir utiliser le digaramme de Voronoï. Ce n'est pas compliqué si je vous l'explique .

Définition : Soit S un ensemble de n sites de l'espace euclidien en dimension d. Pour chaque site p de S, la cellule de Voronoï V(p) de p est l'ensemble des points de l'espace qui sont plus proches de p que de tous les autres sites de S. Le diagramme de Voronoï de V(S) est la décomposition de l'espace formée par les cellules de Voronoï des sites.
Définition : La triangulation de Delaunay de S est le dual géométrique du diagramme de Voronoï de S : deux points de S sont reliés par une arête dans la triangulation de Delaunay si et seulement si leurs cellules sont adjacentes dans le diagramme de Voronoï de S.

Avec un dessin ce sera plus facile :

Ou des formules : 

On se place dans un espace euclidien E. Soit S un ensemble fini de n points de E. Les éléments de S sont appelés centres, sites ou encore germes.

On appelle région de Voronoï ou cellule de Voronoï associée à un élément p de S l’ensemble des points qui sont plus proches de p que de tout autre point de S.

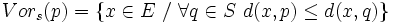
Pour deux points a et b de S, l’ensemble Π(a,b) des points équidistants de a et b est un hyperplan affine (un sous-espace affine de co-dimension 1). Cet hyperplan est la frontière entre l’ensemble des points plus proches de a que de b, et l’ensemble des points plus proches de b que de a.

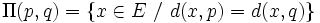
On note H(a,b) le demi espace délimité par cet hyperplan contenant a, il contient alors tout les points plus proches de a que de b. La région de Voronoï associée à a est alors l’intersection des H(a,b) où b parcourt S\{a}.

Les régions de Voronoï sont des polytopes convexes en tant qu’intersection de demi espaces. L’ensemble de tels polygones partitionne E, et est la partition de Voronoï correspondant à l’ensemble S.

En dimension 2 il est facile de tracer ces partitions, on les appelle dans ce cas parfois diagrammes de Voronoi. On se base sur le fait que la frontière entre les cellules de Voronoi de deux germes distincts se situe forcément sur la médiatrice qui sépare ces deux germes. En effet, les points de cette médiatrice sont équidistants des deux germes donc on ne peut pas affirmer qu'il se situent dans l'une ou l'autre cellule de Voronoi. Pour un ensemble de germes, le diagramme de Voronoi se construit donc en déterminant les médiatrices de chaque couple de germes. Un point d'une médiatrice appartient alors à une frontière de Voronoi s'il est équidistant d'au moins deux germes et qu'il n'existe pas de distance plus faible entre ce point et un autre germe de l'ensemble.
Le diagramme de Voronoï est le dual de la triangulation de Delaunay, on peut définir la triangulation de Delaunay à partir du diagramme de Voronoï, deux points p et q créent une arête dans le graphe de Delaunay si et seulement si les régions de Voronoï associées à p et q sont adjacentes.

Donc çà :

Les diagrammes de Voronoï sont des structures très utiles, rencontrées fréquemment car elles permettent de représenter des relations de distance entre objets et des phénomènes de croissance : il n'est pas étonnant de les voir utilisés pour modéliser des cristaux ou les grandes structures de l'univers, et de les trouver souvent dans la nature, par exemple sur la carapace d'une tortue ou sur le cou d'une girafe réticulée. Les diagrammes de Voronoï sont aussi des structures de données permettant de résoudre de nombreux problèmes~: recherche de plus proches voisins et planification de mouvements notamment.

C'est d'accord ?

Alors puisque vous êtes sages et bien attentifs , voilà la réponse :

La commune française (en métropole ) qui porte le point le plus éloigné de la mer est

Artolsheim (Bas-Rhin )

dont la rive sur le Rhin est à près de 430 km( à vol de goéland ) du golfe de Gênes , vers le sud , comme de l'estuaire de l'Escaut,vers le nord .
La méthode revient à chercher en France le centre du plus grand cercle qu'on puisse inscrire  à l'intérieur du tracé des côtes de l'Europe ( ce problème mathématiques se résout grâce au diagramme de Voronoï, et c'est là qu'on le retrouve ) .

Le résultat est très sensible aux critères géographiques et océanographiques  retenus pour définir la notion de limite entre la terre et la mer et , une fois le principe de la côte étant spécifié , à la précision géométrique des données utilisées pour le tracé .

Le jeu des principales variations définit plutôt une zone :
avec Artolshein ,ses limitrophes Schoenau, au nord et Mackensheim au sud , nous avons là les communes françaises les plus éloignées de la mer . A 12 km de Sélestat .

Inspiré d'IGN magazine n°50 . Et c'est sérieux !

Et si vous pensiez que c'était un poisson d'avril , eh bien je vous ai eus. Tout est vrai .   

Cerise violette

Comments

[tanki]

Bon sang, mais c'est bien sûr ;) !!!

[Christel]

Simple comme bonjour !!! Aie ma tête !!!

Bizz :o)

[Bidouillette]

Bon, je ne doute pas, mais ...........tu sais quoi? Je te téléphone, là l'instant et tu me récites tout çà par cœur, que je vois si tu as tout tout bien saisi!!!

Lol, on apprend ici!!!!

Bisous encore plus éloignées de chez toi mais pas de la mer!!!

[Monique 37]

Très interessant!!! MERCI Violette! Je serais moins bête ce soir!
Bises et bon We à toi et à tes peluches!

[Ptisa]

sans tes calculs j'allais dire Colmar ! j'étais pas loin !